1. 서론
단백질은 표현형에 직접적인 관여를 하기 때문에 중요합니다. 그러나 단백질을 정확하게 측정하기 위해서는 많은 요인들 때문에 힘듬니다.
예를 들어 post translational modification (전사후 수정과정)으로 인해서 단백질들이 변화 할수도 있고, 단백질의 특성상 반감기가 짧은 단백질이라던지 등 많은 요인들이 있습니다.
위 같은 요인은 둘째치더라도 조직들의 단백질 양을 이용한 분석을 통해 질병군과 대조군 사이 마커를 찾는다던지 Differential Expression Gene (DEG)가 실제로 단백질양에서도 변화를 일으키는지 등을 보기 위한 연구가 많이 이루어지고 있습니다.
뭐 단순하게 발현이 됬다 안됬다를 보기 위해서는 western blot을 이용하면 되지만 RNA 양을 비교하는것처럼 비교하기 위해서는 샘플들에서 단백질 양을 확인해야 합니다.
단백질 양을 확인하기 위한 방법은 여러가지가 있습니다. 그중에서 우리가 쉽게 데이터를 볼수있는 방법은 Reverse Phase Protein Array (RPPA)와 Mass Spectrometry (MS) 데이터가 아닐까 싶습니다.
둘 다 TCGA에서 실험을 한 데이터를 공개해놓고 있습니다. (MS의 경우 일부 암종에 대해서 데이터가 있습니다.)
간단하게 이 두가지 방법에 대해서 장단점을 설명하고 본론으로 넘어가도록 하겠습니다.
RPPA의 장점으로는 Antibody를 이용하기 때문에 정확한 단백질 양을 확인할 수 있다. 라고 이야기하지만,
반대로 Antibody 기반이기 때문에 확인가능한 유전자가 한정적인 단점이 있습니다.
MS의 장점은 다양한 단백질 데이터를 얻을 수 있지만, 단점은 가격이 비싸고 정확성의 문제가 있는것 같습니다. 뭐 자세한 내용은 생략을 하겠습니다. (저도 대략적으로 알고있고, 추후에 시간이 된다면 자세히 알아보도록 하죠.)
2. 본론
MS에서 단백질 양을 구할때, Missing data가 발생이 무조건 될 수 밖에 없습니다.
이를 해결하기 위해 Imputation 이라는 방법을 사용하는데, 정말 다양한 imputation method가 있습니다.
오늘은 이 imputation방법 중에 어떤 방법이 더 괜찮은 방법인지 실험을 해보도록 하겠습니다.
package는 imp4p라는 package를 이용할 것 입니다.

여기에서는 총 9가지정도 되는 imputation method를 공개 해놓고 있습니다. (mle, slsa, igcda, rand, mi, mix, pa, PCA, rf)
9가지 방법들 중에 어떤 방법이 괜찮은지 나름 평가를 진행하고자 합니다.
테스트 데이터는 cbioportal에 있는 breast MS 데이터를 이용하였습니다.
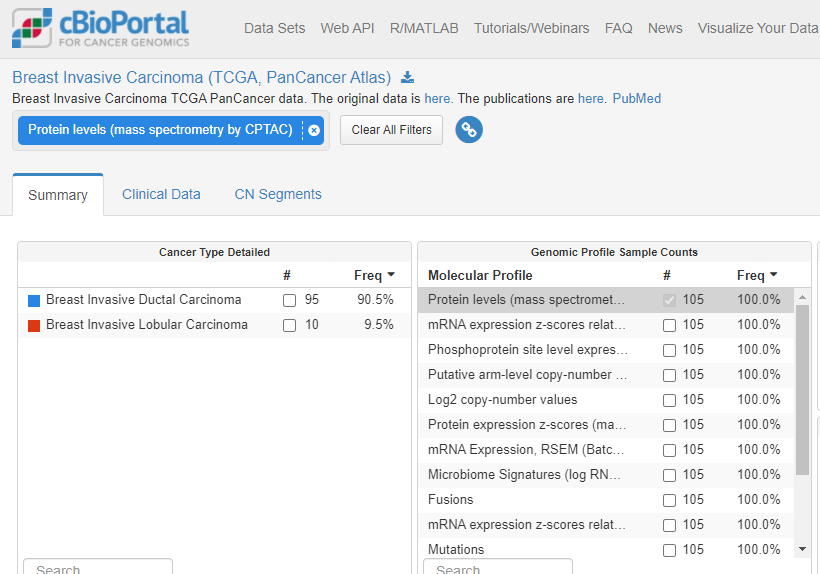
2-1. 준비단계 (preprocessing)
데이터를 읽고, 분포가 어떤지 등을 확인하였습니다.
# cbioportal TCGA MS 데이터 읽기
TCGA<-read.table('./brca_tcga_pan_can_atlas_2018/data_protein_quantification.txt',sep='\t',header=T,stringsAsFactors = F)
# gene name 부분 제거
TCGA1<-TCGA[,2:ncol(TCGA)]
# NA의 분포를 확인하기
con_NA<-list()
for(i in 1:ncol(TCGA1)){
con_NA[[colnames(TCGA1)[i]]]=table(is.na(TCGA1[,i]))
}
con_1<-as.data.frame(con_NA)
rownames(con_1)<-c('False','True')
con_1<-con_1[,grep('Freq',colnames(con_1))]
con_1<-con_1[,order(con_1[2,])]
barplot(height = as.matrix(con_1[2,]))

Missing value의 개수 분포를 보면 샘플당 다양하게 missing value가 있다는 것을 확인할 수가 있습니다.
(MS로 단백질양 비교하려는 분들은 대부분 위와 같은 경우를 많이 보실겁니다.)
Imputation method를 비교해보기 위해 실측값이 있는 상태에서 임의로 missing value를 만들어주었습니다.
# 데이터가 크기 때문에 잘라줍니다.
TCGA1<-na.omit(TCGA1)
TCGA1<-TCGA1[1:3000,]
TCGA1_1<-TCGA1 # TCGA1은 raw data, TCGA1_1는 임의로 missing value를 추가 시킨 데이터
# 임의로 missing data를 늘려서 만듬
mv=50 # 첫 시작 missing value는 50부터
set.seed(1234)
for(i in 1:ncol(TCGA1_1)){
TCGA1_1[sample(nrow(TCGA1_1),mv),i]=NA
mv=mv+1 # missing value 개수를 추가
}
# 제작한 데이터
con_NA<-list()
for(i in 1:ncol(TCGA1_1)){
con_NA[[colnames(TCGA1_1)[i]]]=table(is.na(TCGA1_1[,i]))
}
con_1<-as.data.frame(con_NA)
rownames(con_1)<-c('False','True')
con_1<-con_1[,grep('Freq',colnames(con_1))]
con_1<-con_1[,order(con_1[2,])]
# 임의로 만든 NA 값들 샘플당 분포확인
barplot(height = as.matrix(con_1[2,]))
# condition 세팅
condi<-as.factor(rep(1,ncol(TCGA1_1)))위를 통해서 만든 데이터에서 NA값들의 분포는 다음과 같습니다.

Raw 데이터 보다는 임의적이긴하지만 비슷한 형태를 보이고 있고, Imputation 진행 후에 실측값과 예측값들의 관계를 비교해보도록 하겠습니다.
2-2. 분석단계 (imputation 진행)
먼저 9개의 방법에 대해서 분석을 진행을 하였습니다.
library(imp4p)
TCGA_mle<-impute.mle(TCGA1_1,conditions = condi)
TCGA_slsa<-impute.slsa(TCGA1_1,conditions = condi)
TCGA_igcda=impute.igcda(TCGA1_1,conditions = condi,tab.imp=TCGA_slsa)
TCGA_mi=impute.mi(TCGA1_1,conditions = condi)
##
TCGA_rand=impute.rand(TCGA1_1,conditions = condi)
TCGA_res=estim.mix(TCGA1_1,TCGA_rand,conditions = condi)
TCGA_born=estim.bound(TCGA1_1,conditions = condi)
TCGA_proba=prob.mcar.tab(TCGA_born$tab.upper,TCGA_res)
TCGA_mix=impute.mix(TCGA1_1,prob.MCAR = TCGA_proba,conditions = condi,threshold = 0.5, methodMCAR = 'slsa',methodMNAR = 'igcda',
nknn=15,weight=1,selec='all',ind.comp = 1,progress.bar = T,repbio = 1)
##
TCGA_pa=impute.pa(TCGA1_1,conditions = condi)
TCGA_PCA=impute.PCA(TCGA1_1,conditions = condi)
TCGA_rf=impute.RF(TCGA1_1,conditions = condi)
위 분석하는 도중에 mix, mi의 경우 왜 그런지는 모르겠으나, 실패를 하였고, slsa, rf method의 경우 돌아가는데 오래걸렸습니다. 또한 mle의 경우 약간의 에러가 있었으나, 값이 나온 관계로 그대로 진행하겠습니다.
2-3. 결론 도출단계
일단 다 돌린 후에 임의로 missing value로 만든 위치의 값들을 모조리가져오고, 실측값들을 모조리 가져왔습니다.
TCGA_mle_value<-TCGA_mle[is.na(TCGA1_1)]
TCGA_igcda_value<-TCGA_igcda[is.na(TCGA1_1)]
TCGA_slsa_value<-TCGA_slsa[is.na(TCGA1_1)]
TCGA_rand_value<-TCGA_rand[is.na(TCGA1_1)]
# TCGA_mi_value<-TCGA_mi
# TCGA_mix_value<-TCGA_mix[is.na(TCGA1_1)]
TCGA_pa_value<-TCGA_pa$tab.imp[is.na(TCGA1_1)]
TCGA_PCA_value<-TCGA_PCA[is.na(TCGA1_1)]
TCGA_rf_value<-TCGA_rf[is.na(TCGA1_1)]
# imputation value 정리
result_data<-data.frame(Method=c(rep('mle',length(TCGA_mle_value)),rep('igcda',length(TCGA_igcda_value)),
rep('slsa',length(TCGA_slsa_value)),rep('rand',length(TCGA_rand_value)),
rep('pa',length(TCGA_pa_value)),
rep('PCA',length(TCGA_PCA_value)),rep('rf',length(TCGA_rf_value))),
value=c(TCGA_mle_value,TCGA_igcda_value,TCGA_slsa_value,
TCGA_rand_value,TCGA_pa_value,TCGA_PCA_value,TCGA_rf_value))
result_data1<-data.frame(mle=TCGA_mle_value,igcda=TCGA_igcda_value,slsa=TCGA_slsa_value,
rand=TCGA_rand_value,pa=TCGA_pa_value,
PCA=TCGA_PCA_value,rf=TCGA_rf_value)
imputation값들의 분포를 boxplot으로 보도록 하겠습니다.

mle의 경우 너무 이상하게 나왔고, range를 줄여서 보도록 하겠습니다.

mle를 제외하고 비슷한 범위를 갖는 방법들이 있습니다. (igcda, pa) (PCA, rand, rf, slsa)
그렇다면, 원래 데이터와, 원래 데이터에서 NA를 임의로 넣은 데이터, 그리고 imputation방법 결과 끼리 평균과 표준편차는 어느정도 될까요.
| igcda | mle | pa | PCA | rand | rf | slsa | raw (NA 무) |
raw (NA유) |
|
| mean | -0.87 | 525.3 | -1.91 | -0.017 | -0.02 | -0.01 | -0.02 | -0.01 | -0.01 |
| sd | 0.83 | 224.2 | 0.60 | 0.42 | 0.44 | 0.40 | 0.35 | 0.56 | 0.56 |
raw데이터의 경우 왜그런지는 모르겠지만, 평균과 표준편차가 약간 다른 모습을 보였습니다.
그리고 mle의 경우 너무 예측에 벗어난 경우같고, igcda, pa 또한 예측이 안좋아 보입니다.
마지막으로 임의로 missing 값을 만든 곳에서 원래 값들과 imputation 값들 사이 correlation을 확인해보겠습니다.
real_TCGA<-TCGA1[is.na(TCGA1_1)]
result_data1<-cbind.data.frame(result_data1,obs_value=real_TCGA)
panel.cor <- function(x, y, digits = 2, cex.cor, ...)
{
usr <- par("usr");
on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r <- cor(x, y)
txt <- format(c(r, 0.123456789), digits = digits)[1]
txt <- paste("r = ", txt, sep = "")
if (r > 0.5)
par(bg = "red")
text(0.5, 0.6, txt)
p <- cor.test(x, y)$p.value
txt2 <- format(c(p, 0.123456789), digits = digits)[1]
txt2 <- paste("p = ", txt2, sep = "")
if (p < 0.01) txt2 <- "p < 0.01"
text(0.5, 0.4, txt2)
}
pairs(x = result_data1,lower.panel = panel.smooth,upper.panel = panel.cor)
실제 값과 imputation값들 사이의 correlation을 확인해보았습니다.

결과적으로 보면 rf, PCA, slsa방법의 값들이 실측값과 어느정도 맞는 것으로 확인할 수가 있습니다.
이전에도 TCGA 데이터 이외의 다른 MS 데이터를 이용해서 위와 같은 방법으로 비교를 해봤을 때, rf, PCA, slsa 방법이 실측값 imputation 값이 잘 나왔던 것을 확인하였습니다.
mle의 경우 데이터의 특성에 따라 값이 비슷하게 나오는 경향이 있는 것 같구요. mi, mix의 경우 에러가 나서 결과 확인을 못했지만, 돌리기 어렵기 때문에 사용하기가 좀 예민함이 있는것 같습니다.(아니면 제가 돌리는 방법을 모르던지요.)
그래도 결과적으로는 돌리기 쉬운 방법 + 결과도 잘나오는 방법을 이용하는것이 가장 좋은 것 같습니다.
결과 : PCA, rf, slsa 방법의 imputation이 좋다. (적어도 TCGA ms 데이터에선)
그리고 MS의 imputation 방법들은 대부분 microarray에서 사용하던 방법을 기반으로 제작했었기 때문에 반대로 microarray에다가 적용이 가능할 것 같습니다. (안해봤지만 다음에 기회가 된다면 해보죠.)
'실용적인프로그래밍 > R' 카테고리의 다른 글
| [ggplot2] barplot에서 갭 제거하기 (빈공간제거, 0부터 시작) (0) | 2023.05.18 |
|---|---|
| [ggplot] 여러 개의 그래프를 하나로 합치는 방법 (0) | 2022.04.07 |
| [R] scRepertoire에서 오류 해결 방법 (0) | 2021.11.12 |
| [R] msa package 설치 에러 해결! (gcc) (0) | 2021.08.23 |
| [R error] the given url does not appear to be a valid cran repository (0) | 2021.05.13 |


댓글