machine learning에서 가장 기본적인 linear regression에 대해 포스팅하려고 합니다.
포스팅해야할 주제는 많은데 정리가 잘 안되네요~ ㅎㅎㅎ
요번에 machine learning 관련 내용 멘토링을 하다보니 이 포스팅을 하게 되었습니다. ㅎㅎㅎ
이론적인 내용보다는 어떻게 돌린다 정도로만 포스팅 하도록 하겠습니다. (통계학은 공부중이라 ㅎㅎ)
시작하도록하겠습니다.
우선 linear regression은 단순하게 말해서 종속변수와 독립변수의 관계를 선형식으로 나타낸다! 라고 생각하시면 됩니다. regression이라는 개념은 종속변수를 독립변수로 설명해보자 입니다.
연습용 데이터의 경우 R에서 유명한 package중 하나인 ggplot2에서 포함되어있는 diamonds라는 데이터셑입니다. (이 블로그에서 많이 사용할 데이터셑입니다.)
1. 데이터 불러오기
다음과 같이 데이터를 불러올 수가 있습니다.
> library(ggplot2)
> data("diamonds")
> data1=diamonds
> colnames(data1)
diamond데이터셑에는 생각보다 많은 데이터가 있습니다.
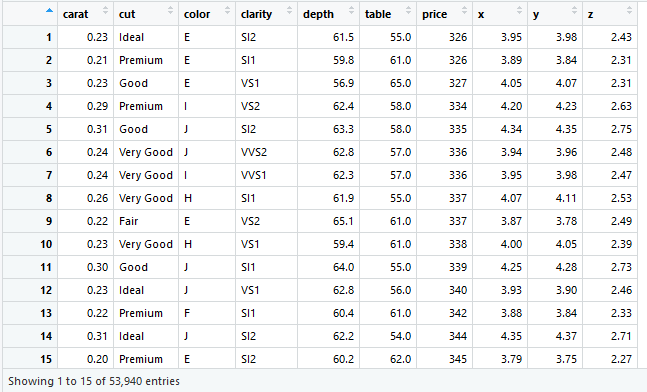
변수들로는 carat, cut, color, clarity, depth, table, price, x, y, z 이렇게 10개의 변수들이 있고, 여기서 우리는 각 변수를 이용하여 가격을 예측하는 모델을 이용을 할 것입니다.
설명하기 쉽게 그냥 숫자로 되어있는 변수들을 이용하여 분석해보도록 하겠습니다.
머신러닝에서 가장 중요한 것은 데이터셑을 나누는 것이죠.
원래는 모델을 만드는 Train Set, 모델을 확인 혹은 점검하는 Test Set, 마지막 점검한 모델을 확인하는 Validation Set 이렇게 3개로 나눕니다. 상황에 따라 Train Set, Test Set 두개로 나누어서 분석을 할 때도 있습니다.
이번 포스팅의 경우 간단한 Linear regression이기 때문에 두 개로 나누어서 분석해보도록 하겠습니다.
2. 데이터 나누기
데이터를 나눌때! 대부분 model에 learning을 더 많이 하기 위해서 train set 규모를 더 크게 합니다.
> set.seed(7054)
> test_sam<-sample(x = nrow(data1),size = nrow(data1)/3)
> test_set<-data1[test_sam,]
> train_set<-data1[-test_sam,]set.seed()는 컴퓨터 내에 랜덤은 사실 랜덤이 아닙니다. 저런 seed숫자에 의해 랜덤될 값들이 정해집니다. set.seed를 설정하는 이유는 여기서 하는 일들의 결과가 다른사람도 같은 결과가 나올수 있게끔 해줍니다.
sample()은 1부터 특정 값(x)사이 size만한 값들을 랜덤으로 뽑아줍니다.
이렇게 train set, test set을 나누었고, 바로 model을 만들어보도록 하죠.
3. Linear regression model 제작
> lm.model<-lm(formula = price~carat+depth+table+x+y+z,data=train_set)
> lm.model
Call:
lm(formula = price ~ carat + depth + table + x + y + z, data = train_set)
Coefficients:
(Intercept) carat depth table x y z
20126.27 10705.98 -192.24 -101.54 -1524.34 267.80 49.83
>
다음과 같이 model이 만들어졌고, Coefficients를 보면 단순하게 1차 함수라고 생각하면 됩니다.
이렇게 model이 만들어졌고, model을 적용해 봅시다!
4. model 적용 및 평가!
model을 평가하는 방법은 주로 2가지가 사용됩니다. 실측값, 예측값 사이 correlation값, Mean squared error(MSE)값
> tr_result<-predict(object = lm.model,newdata = train_set)
> cor(tr_result,train_set$price)
[1] 0.9261971
> cor(tr_result,train_set$price)^2
[1] 0.8578411
> mean(lm.model$residuals^2)
[1] 2253599
>predict()는 다른 종류의 model을 이용할때도 사용이 됩니다. 모델에 있는 종속변수, 독립변수들이 newdata에 들어갈 데이터에 다 포함되어있어야지 돌아갑니다.
cor()는 correlation값을 구할때 사용하는 기능이고, 같은 기능으로서 cor.test()가 있습니다. method를 지정할수가 있어서 default값은 pearson이고 , 추가적으로 spearman, kendall을 확인할 수가 있습니다.
여기서 mean(lm.model$residuals^2)는 실측값 예측값의 차이(residuals)를 제곱하여 평균을 구한다 라는 것입니다. 그거시바로! MES! 제곱의 평균인 이유는 실측값과 예측값 사이 차이가 양수일수도 음수일수도 있기 때문입니다. 그래서 RMSE로도 구하는 경우가 있습니다. MSE에다 root를 씌운거죠!
lm.model이 잘 만들어졌는지 확인하기 위해서는 다음과같은 방법을 사용해도 됩니다.
> summary(lm.model)
Call:
lm(formula = price ~ carat + depth + table + x + y + z, data = train_set)
Residuals:
Min 1Q Median 3Q Max
-23961.2 -618.7 -52.5 344.6 12752.6
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20126.275 537.481 37.446 < 2e-16 ***
carat 10705.982 77.654 137.867 < 2e-16 ***
depth -192.243 6.507 -29.546 < 2e-16 ***
table -101.545 3.789 -26.798 < 2e-16 ***
x -1524.340 63.382 -24.050 < 2e-16 ***
y 267.796 51.087 5.242 1.6e-07 ***
z 49.835 45.776 1.089 0.276
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1501 on 35953 degrees of freedom
Multiple R-squared: 0.8578, Adjusted R-squared: 0.8578
F-statistic: 3.616e+04 on 6 and 35953 DF, p-value: < 2.2e-16
>Multiple R-squared값과, F-검정값들!(regression이 잘 만들어졌나 확인할수있음)등을 확인할 수가 있습니다.
다음으로는 test set에다 적용해 보도록 하겠습니다.
> te_result<-predict(lm.model,test_set)
> cor1<-cor.test(te_result,test_set$price)
> cor1$estimate ## R value
cor
0.9281254
> cor1$estimate^2 ## R value
cor
0.8614168
> cor1$p.value ##
[1] 0
> mean((te_result-test_set$price)^2)
[1] 2223448
>train set과는 다른 방법으로 correlation값과, MSE값을 구해 보았습니다. pvalue가 0인 것은 값이 너무 낮기때문에 0처리가 된 것입니다.
train set에서는 correlation 값이 0.926, test set에서는 0.928입니다. train set보다 test set에서 더 잘맞추네?! 뭔가 잘못된 model인가?! 라고 생각 할 수가 있지만, correlation값은 약간의 차이가 있을 수가 있기 때문에 저정도의 차이는 괜찮다고 봅니다.
두 Correlation 값의 차이가 0.1이상 차이가 나면 뭔가 이상하다 생각할 수가 있죠. (sampling 오류인가?, under fitting인가? 를 고려해보셔야 합니다.)
여기까지가 Linear regression 엄밀히 말하면 Multiple Linear regression을 어떻게 돌리는지에 대해서 이야기해 보았습니다!
끝내려고 했으나!! 그래도 좀 추가적으로 내용을 씁니다.!
가격을 예측하는데 독립변수들이 얼만큼 예측을 할 수가 있는지 Single Linear regression을 구해서 확인해 보도록 하겠습니다. (그냥 궁금해서 해보는겁니다.)
> diamonds_1<-diamonds[,c('price','carat','depth','table','x','y','z')]
> set.seed(7054)
> test_sam<-sample(x = nrow(diamonds_1),size = nrow(diamonds_1)/3)
> test_set<-diamonds_1[test_sam,]
> train_set<-diamonds_1[-test_sam,]
>
> x1<-c() # train cor
> x2<-c() # test cor
> y1<-c() # train mse
> y2<-c() # test mse
>
> for(i in 1:(ncol(diamonds_1)-1)){
+ lm.model<-lm(as.formula(paste0('price~',colnames(diamonds_1)[i+1])),data=train_set)
+ tr_result<-predict(lm.model,newdata = train_set)
+ te_result<-predict(lm.model,newdata = test_set)
+ tr_mse<-mean((tr_result-train_set$price)^2)
+ te_mse<-mean((te_result-test_set$price)^2)
+ x1<-c(x1,cor(tr_result,train_set$price))
+ x2<-c(x2,cor(te_result,test_set$price))
+ y1<-c(y1,tr_mse)
+ y2<-c(y2,te_mse)
+
+ }
>
> par(mfrow=c(2,1),oma=c(1,1,1,1),mar=c(1,4,2,1))
> plot(NA,xlim = c(1,6),ylim=c(0,1),xlab = 'Variable',ylab = 'Correlation Obs vs Pred',xaxt='n',main='Single Linear regression')
> axis(1,at=c(1:6),labels = colnames(diamonds_1)[2:ncol(diamonds_1)])
> lines(c(1:6),x1,col='red')
> lines(c(1:6),x2,col='blue')
> grid()
> legend('bottomright',lty=1,col=c('red','blue'),legend = c('Train Set','Test Set'))
>
>
> plot(NA,xlim = c(1,6),ylim=c(min(c(range(y1),range(y2))),max(c(range(y1),range(y2)))),xlab = 'Variable',ylab = 'Mean Squared Error, MSE',xaxt='n')
> axis(1,at=c(1:6),labels = colnames(diamonds_1)[2:ncol(diamonds_1)])
> lines(c(1:6),y1,col='red')
> lines(c(1:6),y2,col='blue')
> grid()
> legend('topright',lty=1,col=c('red','blue'),legend = c('Train Set','Test Set'))
> 코드 해석은 천천히 한줄씩 보시면 알게 됩니다...
결과로 나온 그래프는 다음과 같습니다.

결과를 보니 굳이 Multiple 변수를 사용하지 않아도 carat이나, x값만 이용해서 예측하면 대략적인 값을 알 수가 있음을 확인할 수가 있네요.!
자 이제 정말로 마치겠습니다.
다음에는 다른 machine learning방법을 알아오도록 하겠습니다! (SVR? or Random forest regression?)
'실용적인프로그래밍 > R' 카테고리의 다른 글
| [R] ggplot2 - Scatter plot (0) | 2020.07.22 |
|---|---|
| [R] ggplot - pair plot 그려보기 (ggplot 기초, gridExtra, ggfittext) (0) | 2020.07.21 |
| [R] ggplot2 package 기초 (qplot, ggplot) (0) | 2020.07.20 |
| [R] Machine learning (3) - Support vector machine (SVR, part2) (2) | 2020.07.10 |
| [R] Machine learning (2) - Support vector machine (SVM, part 1) (5) | 2020.07.09 |



댓글